Reverse gradient searching for turning point

This note summerizes using a simple and efficient trick: reverse gradient searching for finding turning points in noisy cases.

Background

Two basic methods: 1. taking maximum. 2. take zero crossing points for gradient of the signal. Here are sample codes.

# get max points
def get_max_point(y):
    y_max = np.max(y)
    y_max_index = np.where(y == y_max)[0]
    if y_max_index.shape[0] > 1:
        y_max_index = y_max_index[0]
    return y_max_index, y_max

# the zero crossing points from gradient
def get_gradient_zero_point(y):
    # calculate gradient
    y_gradient = np.gradient(y)
    # detect zero crossings
    zero_crossings = np.where(np.diff(np.sign(y_gradient)))[0]
    return zero_crossings

Example results

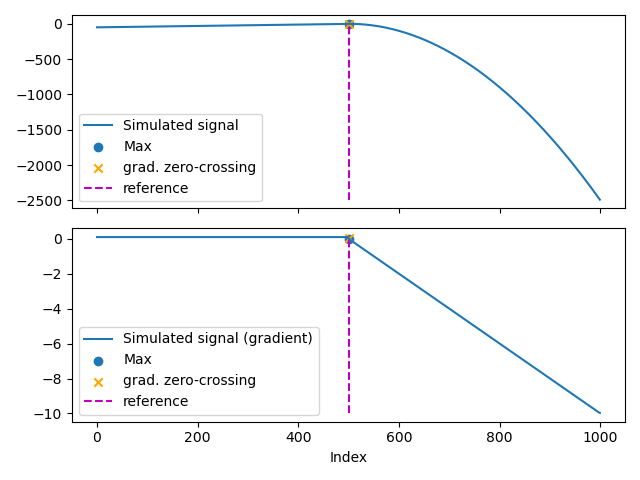
We first simulate signal in a simple case. In this case, turning point can be detected using maximun point detection and detecting zero-crossing for gradient.

# simulate a curve with turning point
x = np.arange(0, 1000, 1)
y_first_half =  0.1* (x[0:500] - 500)
y_second_half = - (x[500:] - 500)**2 * 0.01
y_concatinate = np.concatenate([y_first_half,y_second_half], axis=0)

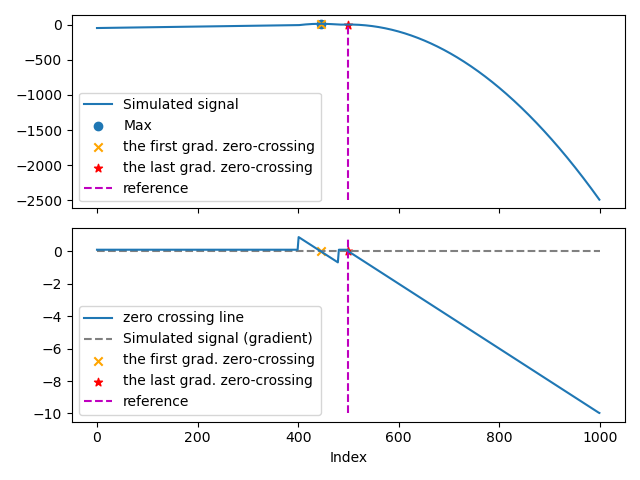
Add some changes before the reference turning point (in the middle), and maximun is no longer around the reference turning point. Zero crossing points are no longer unique.

y_noise =-0.01* (x[400:480] - 440)**2 
y_noise = y_noise - np.min(y_noise)

y_concatinate_add_fusion = y_concatinate.copy()
y_concatinate_add_fusion[400:480] = y_concatinate_add_fusion[400:480] + y_noise

In this case, we can’t use maximum point detection. The last turning point returns the reference turning point.

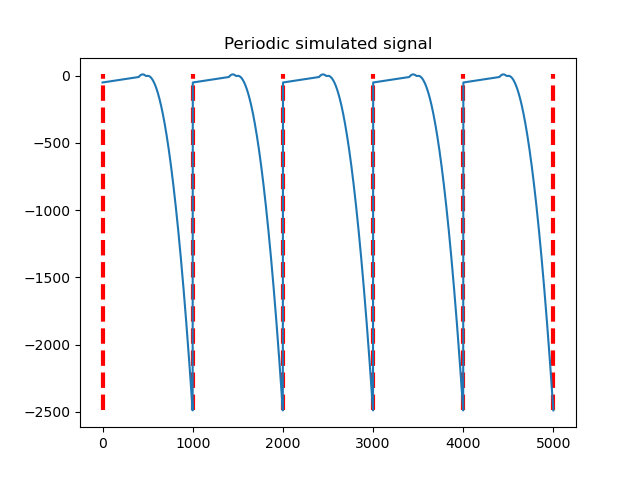
Algorithm lagging window size for periodic signals

The lagging window size for running the algorithm off-line is the same as maximun detection, which is the period of periodic signals (indicated by dotted line here). If signal are isolating (no fix period), the worst case is the lagging window equals to max interval of each isolated segments.