Time series clustering using tslearn

TSlearn package for classic timeseries clustering methods.

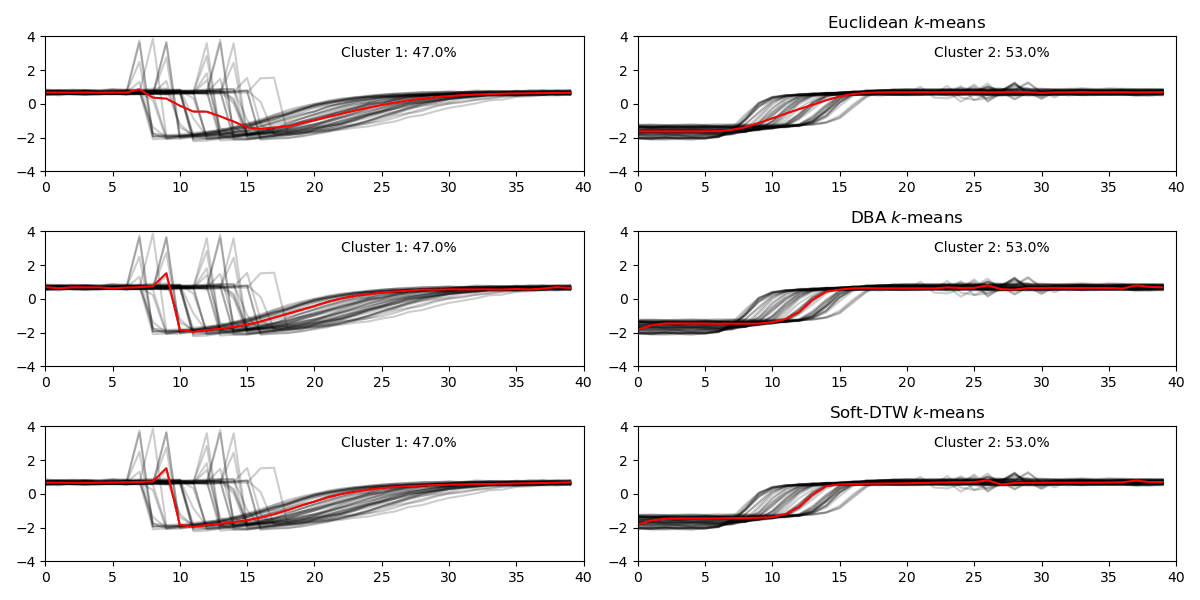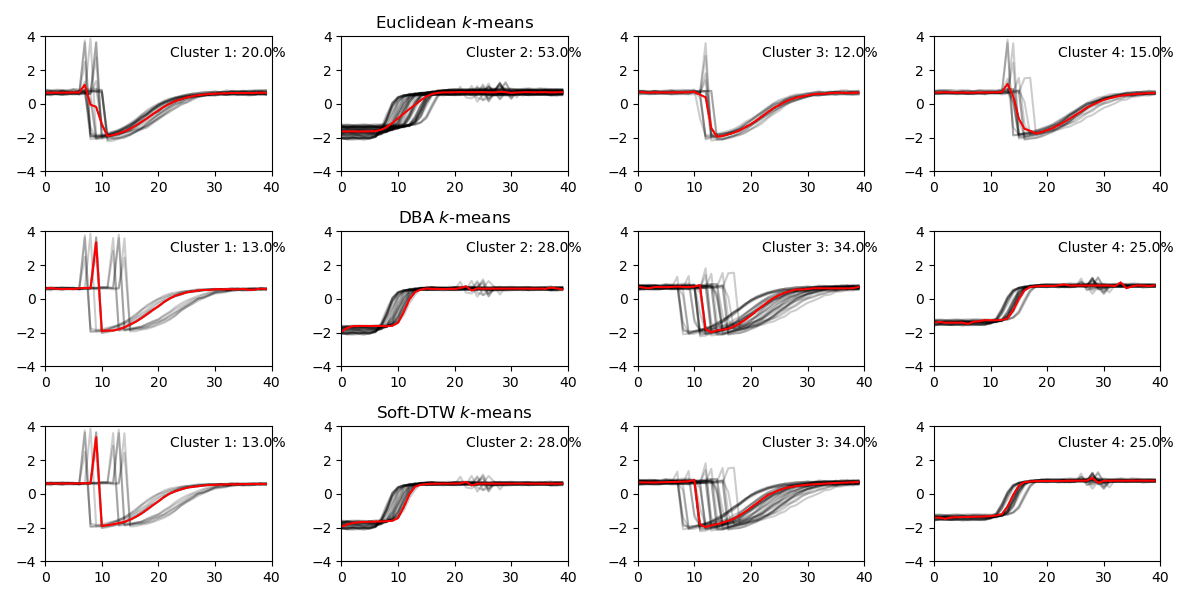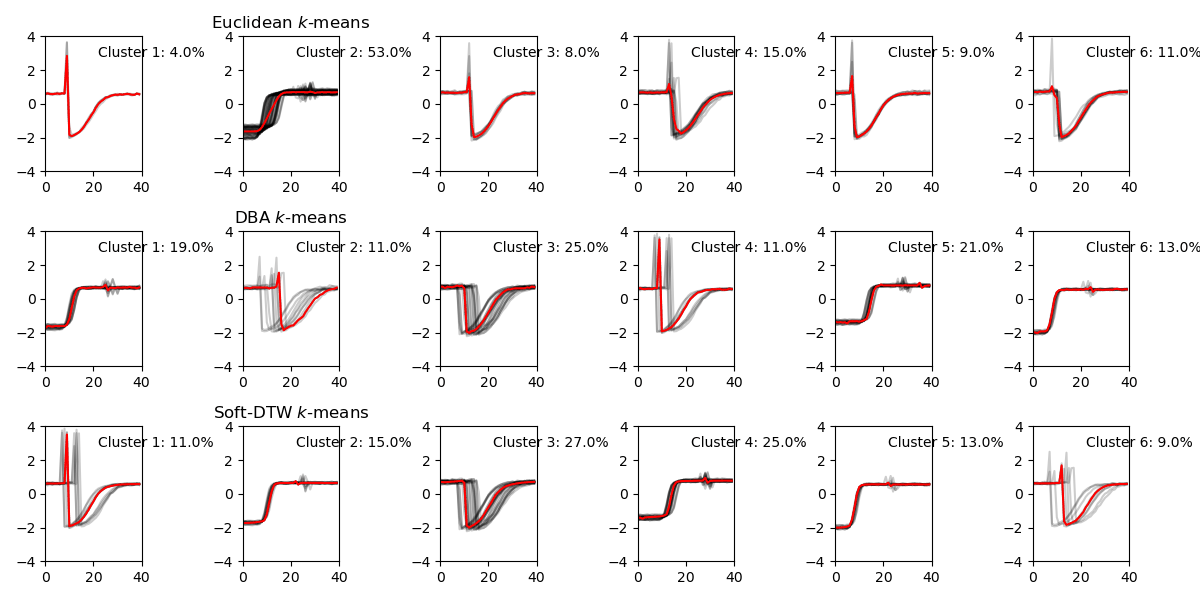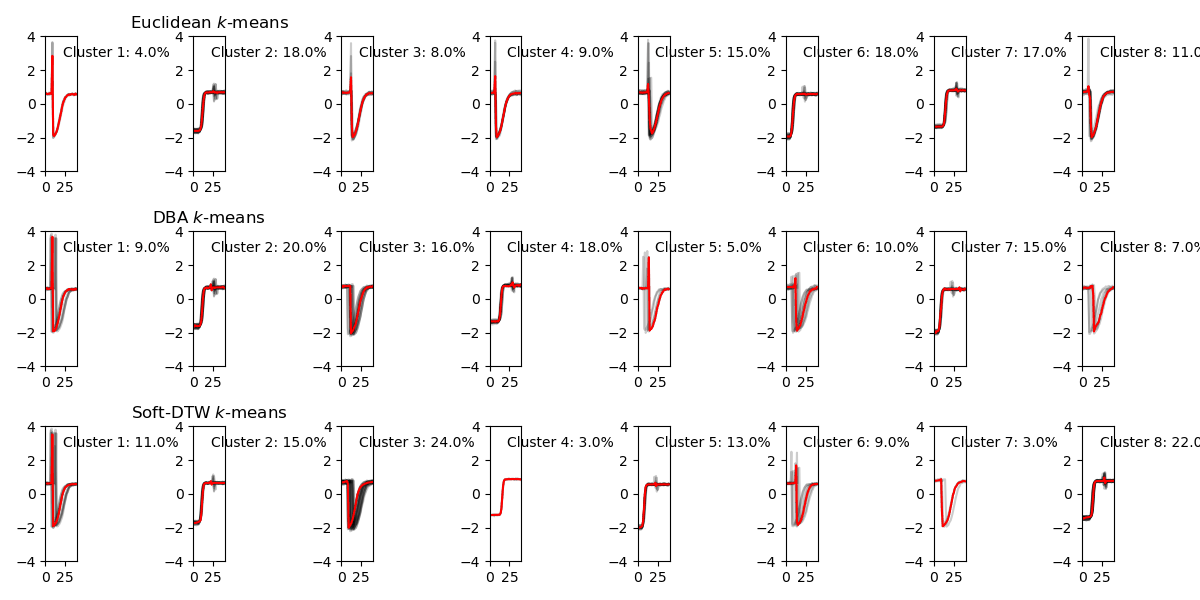
I followed this demo. With some small modifications (parameters stated in last section, and then the following results with number of clusters set to nc = 3 is generated.

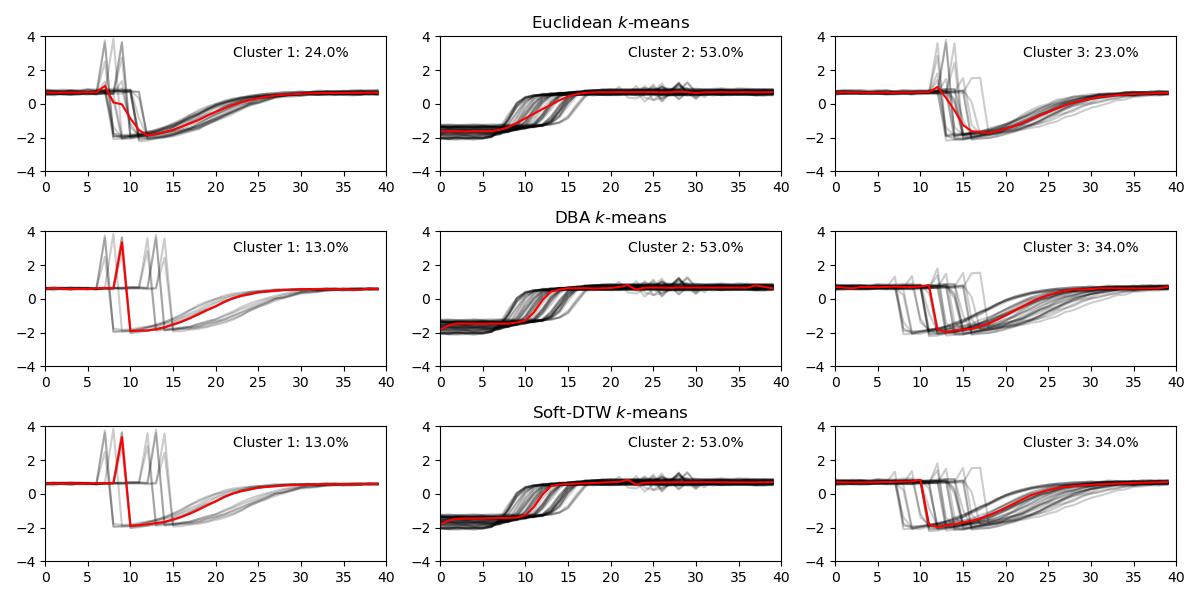
Methods:

$\bullet$ Euclidean k-means

$\bullet$ DTW (Dynamic Time Wrapping). Here, we use DTW with Barycenter Averaging (DBA).

$\bullet$ Soft-DTW

Remarks:

One needs to fill in missing data (if there are) first before using those algorithms.

Clustering series needs to have equal length. If not, resampling needs to be done before applying those algorithms.

timeseries k-means clustering center is a smoothed/low-passed version of signals in each cluster.

DTW deals with time-invariance better, therefore DTW clustering centers are more indicative of shape.

DBA/DTW and Soft-DTW results are reasonably similar. Soft-DTW has differentiable loss.

Cluster size changes with different number of clusters

Below image shows how cluster size changes with various numnber of clusters. The sample size is n=100 to train cluster algorithms, and time dimension is t = 40. In this dataset, the number of labels in the dataset is 4.

Among three methods, when increasing the number of clusteres, k-means generates clusters with large size differences.

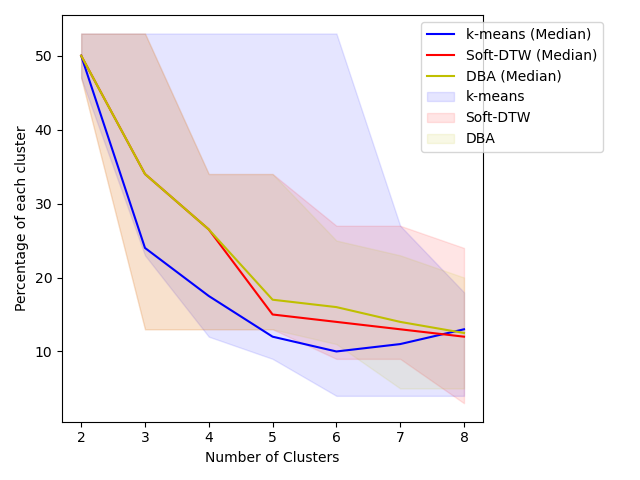
Here is a visualization of varing the number of clusters for three methods. At the start, when the number of clusters nc = 2, all three methods give similar clustering results. While increasing nc, K-means method doesn’t start dividing majority cluster: Cluster 2 until nc is very large at nc=6. Overall, DBA and Soft-DTW have very similar results, especially when number of clusters is small.

Performance measurements

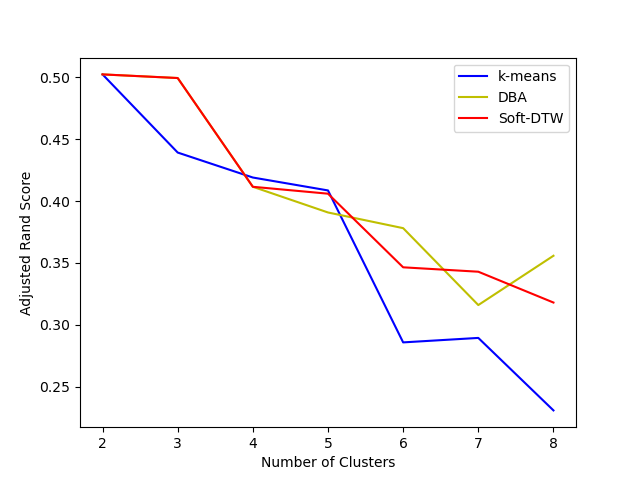
Performance measure for clustering algorithm is a subjective matter. In a easier case if there is true label, which may not be true for a lot of applications, there are measures can be used.

The following results uses Adujusted Rand Score/Index (ARI) ARI is symmetric.

In this example, since k-means tends to have the over-dividing behavior, its ARI drops faster than other DTW-based methods. It also explains that small number of clusters nc scores better in terms of ARI.

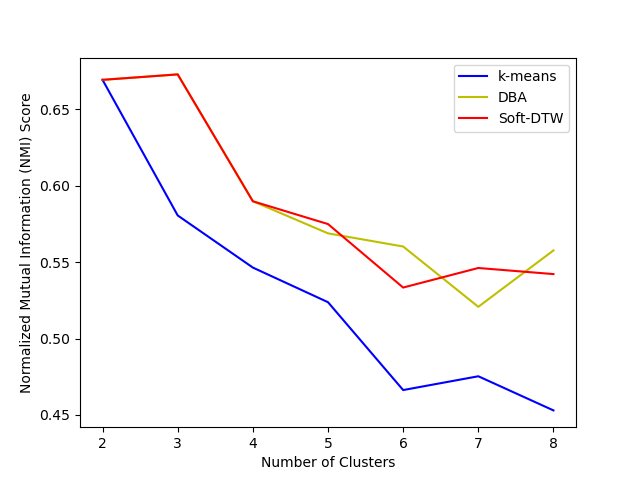
Other metrics include Normalized Mutual Information (NMI). In this cases, NMI suggests consistent favor of DTW-based methods compared to k-means varing number of clusters.

Additional readings regarding clustering such as elbow method for selecting optimal number of clusters.

Appendix:

Example of ARI score: it penalizes the behavior for dividing one cluster into smaller clusters. For example,

# ARI examples
from sklearn.metrics.cluster import adjusted_rand_score
>>> adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 1])
 0.57

>>> adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 0])
0.33 

>>> adjusted_rand_score([0, 0, 0, 0], [0, 1, 2, 3])
0.0