notes for deep one-class classification

Notes for reading paper: learning and evaluating representations for deep one-class classification link.

One class classification identifies if an example is the same distribution as training data or not.

• anomaly detection
• outlier detection
• in case of lack of data (not compariable quality) from negative class such as lack of amount, variations in negative class

problems of using contrasive loss directly in one-class classification

• Contrastive loss:

  $L_{cls} = - E_{x, x’ ~ P_X A, A’} log\frac{exp (\tau^{-1} \phi^T(A(x)) \phi(A’(x)))}{ exp ( \tau^{-1} \phi^T(A(x)) \phi(A’(x))) ) + \sum_{i=1}^{M -1} exp ( \tau^{-1} \phi^T(A(x)) \phi(A’(x_i))) ) } \ (1), $

  where

  1. $x_i \neq x$;

  2. $A$ and $A’$ are identical but independent stochastic augmentation processes for two different realizations of $x$;

  3. $\phi (\cdot) $ is a normalization function, $s.t.$ $|| \phi (\cdot) || = 1.$

  In summary, $L_{clr}$ regularizes

  • representations of the same instance with different views $(A(x),A’(x))$ to be similar,
  • those of different instances $(A(x),A’(x_i \neq x))$ to be unlike.

• Class collision:

  The contrastive loss in Eq.(1) is minimized by maximizing the distance between representations of negative pairs $(x,x_i),x \neq x_i$, even though they are from the same class when applied to the one-class classification. This seems to contradict to the idea of deep one-class classification,which learns representations by minimizing the distance between representations with respect to the center $E (g ( f(x) ) - c)$.

• Asymptotic Uniformity (good for powerful representation learning, bad for distingush inlier and outlier):

  When $M \rightarrow \infty$, the optimal solution of denominator of Eq (1) makes uniformity shown in here. Basically, while increasing training data batch size, feature representation tends to be in senario (a), making inlier and outlier not distinguishable. This work would like distribution augmentation case like (c). In another words, this work would like to promote clustering behavior for different augmentation types.

  
  

Graph representations of differences of this proposal to CLR

A graph representation of the original contrastive learning: CLR vs CLR with distribution augmentation for one-class classification problems. Bottom panel picture is from the original paper and the top panel is revised from that picture.”

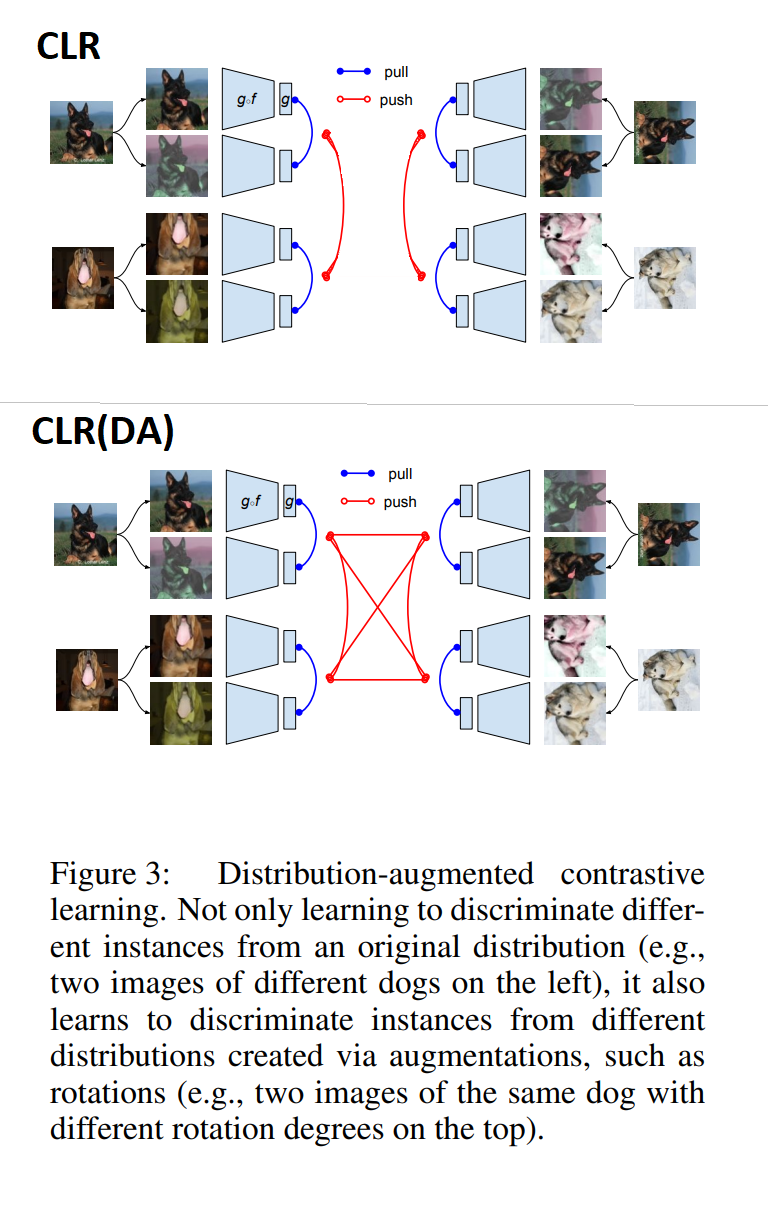
Main proposal from this work

Two step process:

• Step 1: self-supervised learning $x \rightarrow f(x) \rightarrow g(f(x)) $ over a union of distributions.

• Step 2: feed step 1 to a shallow one-class classifier (One-class SVM/OC-SVM, Kernal Density Estimation/KDE).

  Example of KDE for one-class classfication.

Main results:

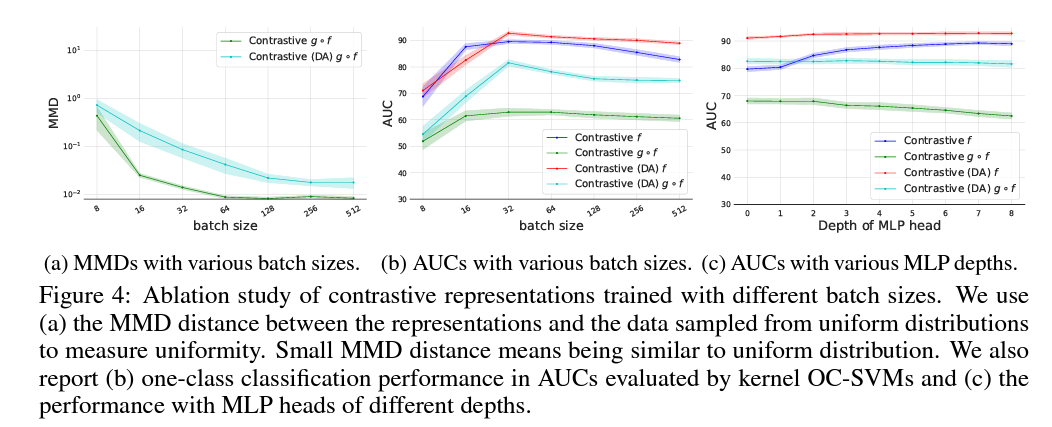
Here $f$ is feature extractor (this paper uses Res-Net) and $g$ is projection head (this paper uses MLP). Authors find that $f$, an input to the projection head, performs better on the downstream task than $g(f(\cdot))$. As in Figure 4c, the performance of $f$ improves with deeper MLP head, while $g(f(\cdot))$ degrades, as it overfits to the proxy task.

Details of can be found in: paper link, code repo.